Per a explicar aquest apartat partirem d’un cas pràctic: Agafem com a exemple el moviment de l’EURUSD i triem com a període de càlcul el d’una hora.
Hem de tenir en compte que podriem haver agafat qualsevol període per a fer l’exemple (un minut, 5 minuts, una setmana, etc.).
Agafem com a preu la mitjana entre el preu ask i el preu bid.
Calculem la variació horària del moviment de l’EURUSD d’un dia qualsevol.
| Variació horària | |||||
| Hora | Ask | Bid | Preu | En preu | En Pips |
| 1:00:00 | 1,08117 | 1,08115 | 1,08116 | 0,00000 | 0 |
| 2:00:00 | 1,08215 | 1,08212 | 1,08214 | 0,00097 | 97,5 |
| 3:00:00 | 1,08187 | 1,08184 | 1,08186 | -0,00028 | -28 |
| 4:00:00 | 1,08171 | 1,08170 | 1,08171 | -0,00015 | -15 |
| 5:00:00 | 1,08140 | 1,08137 | 1,08139 | -0,00032 | -32 |
| 6:00:00 | 1,08124 | 1,08122 | 1,08123 | -0,00015 | -15,5 |
| 7:00:00 | 1,08091 | 1,08091 | 1,08091 | -0,00032 | -32 |
| 8:00:00 | 1,08127 | 1,08126 | 1,08127 | 0,00036 | 35,5 |
| 9:00:00 | 1,08112 | 1,08110 | 1,08111 | -0,00016 | -15,5 |
| 10:00:00 | 1,08162 | 1,08156 | 1,08159 | 0,00048 | 48 |
| 11:00:00 | 1,08108 | 1,08105 | 1,08107 | -0,00052 | -52,5 |
| 12:00:00 | 1,08189 | 1,08187 | 1,08188 | 0,00081 | 81,5 |
| 13:00:00 | 1,08132 | 1,08129 | 1,08131 | -0,00057 | -57,5 |
| 14:00:00 | 1,08129 | 1,08127 | 1,08128 | -0,00002 | -2,5 |
| 15:00:00 | 1,08221 | 1,08199 | 1,08210 | 0,00082 | 82 |
| 16:00:00 | 1,08356 | 1,08354 | 1,08355 | 0,00145 | 145 |
| 17:00:00 | 1,08308 | 1,08306 | 1,08307 | -0,00048 | -48 |
| 18:00:00 | 1,08379 | 1,08376 | 1,08378 | 0,00071 | 70,5 |
| 19:00:00 | 1,08408 | 1,08406 | 1,08407 | 0,00029 | 29,5 |
| 20:00:00 | 1,08415 | 1,08412 | 1,08414 | 0,00006 | 6,5 |
| 21:00:00 | 1,08374 | 1,08373 | 1,08374 | -0,00040 | -40 |
| 22:00:00 | 1,08408 | 1,08372 | 1,08390 | 0,00016 | 16,5 |
| 23:00:00 | 1,08407 | 1,08395 | 1,08401 | 0,00011 | 11 |
| 0:00:00 | 1,08421 | 1,08421 | 1,08421 | 0,00020 | 20 |
La distribució estadística que més s’apropa al moviment de la variació de preus és la distribució normal.
La distribució normal té una sèrie de característiques que s’aprofiten per al càlcul quantitatiu d’actius financers donada la seva aproximació al moviment real d’aquests.
El cas més clar és la volatilitat.
La volatilitat va associada al concepte de desviació estàndard d’una distribució normal.
Nota. Aplicarem la fórmula de la “Desviació Estàndard Mostral” que canvia lleugerament respecte a la de la “Desviació Estàndard Poblacional”.
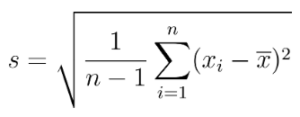
s · Desviació estàndard mostral.
n · Grandària de la mostra.
xi · Observacions de la mostra.
x̄ · Mitjana de la mostra.
Per exemple, tenint en compte la mostra horària de variacions de preu anterior (en pips) tenim els següents resultats:
| n | 24 |
| x̄ | 12,71 |
| ∑(xᵢ – x̄)² | 63771,96 |
I la desviació estàndard és de: 52,66 pips (0.0005266 $).
Segons la regla empírica i de forma aproximada, en una distribució normal:
El 68% de les observacions es troben dins d’una desviació estàndard de la mitjana.
El 95% de les observacions es troben dins de dues desviacions estàndard de la mitjana.
El 99.7% de les observacions es troben dins de tres desviacions estàndard de la mitjana.
Ara imaginem que ens interessa saber el moviment del preu del EURUSD d’aquí un mes si es mantenen les condicions actuals.
Per a traslladar la desviació típica d’un període a un altre usem l’arrel del període.
Exemple, si la variació horària que hem calculat té una desviació de 52,66 pips i volem calcular la que podria tenir de forma mensual, multipliquem per un factor que correspon a l’arrel quadrada de les hores que té un mes.
Suposant un mes de 30 dies i quatre setmanes, sabent que l’EURUSD haurà funcionat els 5 dies feiners tenim que un mes tindrà (30 – 4*2) * 24 = 528 hores. Per tant:
![]()
Per tant, d’aquí a un més la possibilitat de que l’EURUSD es mantingui entre els següents valors: 1,08421 ± 0,01210 és de 68%.
Com veiem, usar la distribució normal com a aproximació del moviment de la variació del preu és molt útil per a fer suposicions.
Hem de tenir en compte que he suposat que la mitjana de les variacions del preu de l’EURUSD és igual o molt propera a zero. Cosa que implica que considerem el seu moviment com a aleatori (estocàstic).
La distribució Lognormal i la volatilitat
Si considerem que el moviment dels preus s’acosta a una distribució lognormal (més que no pas a una distribució normal) podem deduir que la variació del logaritme neperià dels preus segueix una distribució normal.
Per tant, si en l’apartat anterior partiem de la diferència dels preus per a calcular la desviació estàndard, ara partirem de la diferència dels logaritmes neperians dels preus per a calcular la desviació estàndard.
Continuem amb l’exemple anterior:
| Hora | Ask | Bid | Preu | Ln Preu | Variació horària |
| 1:00:00 | 1,08117 | 1,08115 | 1,08116 | 0,07803 | 0 |
| 2:00:00 | 1,08215 | 1,08212 | 1,08214 | 0,07894 | 0,00090 |
| 3:00:00 | 1,08187 | 1,08184 | 1,08186 | 0,07868 | -0,00026 |
| 4:00:00 | 1,08171 | 1,08170 | 1,08171 | 0,07854 | -0,00014 |
| 5:00:00 | 1,08140 | 1,08137 | 1,08139 | 0,07824 | -0,00030 |
| 6:00:00 | 1,08124 | 1,08122 | 1,08123 | 0,07810 | -0,00014 |
| 7:00:00 | 1,08091 | 1,08091 | 1,08091 | 0,07780 | -0,00030 |
| 8:00:00 | 1,08127 | 1,08126 | 1,08127 | 0,07813 | 0,00033 |
| 9:00:00 | 1,08112 | 1,08110 | 1,08111 | 0,07799 | -0,00014 |
| 10:00:00 | 1,08162 | 1,08156 | 1,08159 | 0,07843 | 0,00044 |
| 11:00:00 | 1,08108 | 1,08105 | 1,08107 | 0,07795 | -0,00049 |
| 12:00:00 | 1,08189 | 1,08187 | 1,08188 | 0,07870 | 0,00075 |
| 13:00:00 | 1,08132 | 1,08129 | 1,08131 | 0,07817 | -0,00053 |
| 14:00:00 | 1,08129 | 1,08127 | 1,08128 | 0,07815 | -0,00002 |
| 15:00:00 | 1,08221 | 1,08199 | 1,08210 | 0,07890 | 0,00076 |
| 16:00:00 | 1,08356 | 1,08354 | 1,08355 | 0,08024 | 0,00134 |
| 17:00:00 | 1,08308 | 1,08306 | 1,08307 | 0,07980 | -0,00044 |
| 18:00:00 | 1,08379 | 1,08376 | 1,08378 | 0,08045 | 0,00065 |
| 19:00:00 | 1,08408 | 1,08406 | 1,08407 | 0,08072 | 0,00027 |
| 20:00:00 | 1,08415 | 1,08412 | 1,08414 | 0,08078 | 0,00006 |
| 21:00:00 | 1,08374 | 1,08373 | 1,08374 | 0,08041 | -0,00037 |
| 22:00:00 | 1,08408 | 1,08372 | 1,08390 | 0,08057 | 0,00015 |
| 23:00:00 | 1,08407 | 1,08395 | 1,08401 | 0,08067 | 0,00010 |
| 0:00:00 | 1,08421 | 1,08421 | 1,08421 | 0,08085 | 0,00018 |
La variació horària és la observació mostral que usarem per a calcular la desviació estàndard.
Un apunt, la variació horària l’hem calculat a partir de la variació del logaritme neperià del preu actual i el logaritme neperià del preu anterior. Coneixent el càlcul de logaritmes podem deduir que podriem haver calculat la variació fent el logaritme neperià del preu actual dividit pel preu anterior. I, el més important, el resultat s’assemblaria molt si ho haguessim calculat de la següent manera: Diferència del preu actual i l’anterior dividit entre la mitjana del preu actual i el preu anterior.
En definitiva, la variació que hem calculat no deixa de ser una variació en tant per u dels preus (multiplicant per cent tindriem una variació percentual del preu).
Ara en calculem la desviació estàndard usant la fórmula que ja coneixem: 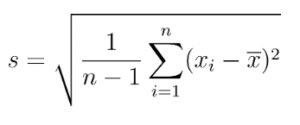
| n | 24 |
| x̄ | 0,000117378 |
| ∑(xᵢ – x̄)² | 0,000005445 |
| s horària | 0,000486555 |
| s mensual | 0,01118019203 |
La desviació estàndard d’aquesta distribució expressada en tant per cent la coneixem com a volatilitat.
La desviació horària és de 0,000486555 i la mensual (multiplicant per l’arrel de 528) és de 0,01118. Per tant, i multiplicant per 100, podem dir que la volatilitat horària és de 0.05% i la mensual, de 1,12%.
En definitiva, hi ha un 68% de possibilitats que el preu de l’EURUSD s’hagi mogut dins del marge de ±1,12% a finals d’aquest mes.
Hi ha un 95% de possibilitats que el preu de l’EURUSD s’hagi mogut dins del marge de ±2,24% a finals d’aquest mes.
Hi ha un 99,7% de possibilitats que el preu de l’EURUSD s’hagi mogut dins del marge de ±3,36% a finals d’aquest mes.
Quan ens parlen que l’EURUSD té una volatilitat anual de 4% podem fer l’exercici invers al què hem fet fins ara i averiguar quina volatilitat mensual seria:
Volatilitat anual = 4%
Volatilitat mensual = Volatilitat anual / SQR(12) = 1,15%