Para explicar este apartado partiremos de un caso práctico: Cogemos como ejemplo el movimiento del EURUSD y elegimos como período de cálculo el de una hora.
Debemos tener en cuenta que podríamos haber cogido cualquier período para hacer el ejemplo (un minuto, 5 minutos, una semana, etc.).
Cogemos como precio la media entre el precio ask y el precio bid.
Calculamos la variación horaria del movimiento del EURUSD de un día cualquiera.
| Variación horaria | |||||
| Hora | Ask | Bid | Precio | En precio | En Pips |
| 1:00:00 | 1,08117 | 1,08115 | 1,08116 | 0,00000 | 0 |
| 2:00:00 | 1,08215 | 1,08212 | 1,08214 | 0,00097 | 97,5 |
| 3:00:00 | 1,08187 | 1,08184 | 1,08186 | -0,00028 | -28 |
| 4:00:00 | 1,08171 | 1,08170 | 1,08171 | -0,00015 | -15 |
| 5:00:00 | 1,08140 | 1,08137 | 1,08139 | -0,00032 | -32 |
| 6:00:00 | 1,08124 | 1,08122 | 1,08123 | -0,00015 | -15,5 |
| 7:00:00 | 1,08091 | 1,08091 | 1,08091 | -0,00032 | -32 |
| 8:00:00 | 1,08127 | 1,08126 | 1,08127 | 0,00036 | 35,5 |
| 9:00:00 | 1,08112 | 1,08110 | 1,08111 | -0,00016 | -15,5 |
| 10:00:00 | 1,08162 | 1,08156 | 1,08159 | 0,00048 | 48 |
| 11:00:00 | 1,08108 | 1,08105 | 1,08107 | -0,00052 | -52,5 |
| 12:00:00 | 1,08189 | 1,08187 | 1,08188 | 0,00081 | 81,5 |
| 13:00:00 | 1,08132 | 1,08129 | 1,08131 | -0,00057 | -57,5 |
| 14:00:00 | 1,08129 | 1,08127 | 1,08128 | -0,00002 | -2,5 |
| 15:00:00 | 1,08221 | 1,08199 | 1,08210 | 0,00082 | 82 |
| 16:00:00 | 1,08356 | 1,08354 | 1,08355 | 0,00145 | 145 |
| 17:00:00 | 1,08308 | 1,08306 | 1,08307 | -0,00048 | -48 |
| 18:00:00 | 1,08379 | 1,08376 | 1,08378 | 0,00071 | 70,5 |
| 19:00:00 | 1,08408 | 1,08406 | 1,08407 | 0,00029 | 29,5 |
| 20:00:00 | 1,08415 | 1,08412 | 1,08414 | 0,00006 | 6,5 |
| 21:00:00 | 1,08374 | 1,08373 | 1,08374 | -0,00040 | -40 |
| 22:00:00 | 1,08408 | 1,08372 | 1,08390 | 0,00016 | 16,5 |
| 23:00:00 | 1,08407 | 1,08395 | 1,08401 | 0,00011 | 11 |
| 0:00:00 | 1,08421 | 1,08421 | 1,08421 | 0,00020 | 20 |
La distribució estadística que més s’apropa al moviment de la variació de preus és la distribució normal.
La distribución normal tiene una serie de características que se aprovechan para el cálculo cuantitativo de activos financieros dada su aproximación al movimiento real de éstos.
Lo más claro es la volatilidad.
La volatilidad va asociada al concepto de desviación estándar de una distribución normal.
Nota. Aplicaremos la fórmula de la “Desviación Estándar Muestral” que cambia ligeramente respecto a la de la “Desviación Estándar Poblacional”.
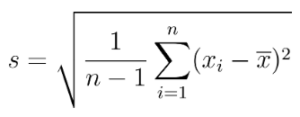
s · Desviación estándard mostral.
n · Tamaño de la muestra.
xi · Observaciones de la muestra.
x̄ · Media de la muestra.
Por ejemplo, teniendo en cuenta la muestra horaria de variaciones de precio anterior (en pips) tenemos los siguientes resultados:
| n | 24 |
| x̄ | 12,71 |
| ∑(xᵢ – x̄)² | 63771,96 |
Y la desviación estándar es de: 52,66 pips (0.0005266$).
Según la regla empírica y de forma aproximada, en una distribución normal:
El 68% de las observaciones se encuentran dentro de una desviación estándar de la media.
El 95% de las observaciones se encuentran en dos desviaciones estándar de la media.
El 99.7% de las observaciones se encuentran en tres desviaciones estándar de la media.
Ahora imaginamos que nos interesa saber el movimiento del precio del EURUSD en un mes si se mantienen las condiciones actuales.
Para trasladar la desviación típica de un período a otro usamos la raíz del período.
Ejemplo, si la variación horaria que hemos calculado tiene una desviación de 52,66 pips y queremos calcular la que podría tener de forma mensual, multiplicamos por un factor que corresponde a la raíz cuadrada de las horas que tiene un mes.
Suponiendo un mes de 30 días y cuatro semanas, sabiendo que el EURUSD habrá funcionado los 5 días laborables tenemos que un mes tendrá (30 – 4*2) * 24 = 528 horas. Por tanto:
![]()
Por tanto, dentro de uno más la posibilidad de que el EURUSD se mantenga entre los siguientes valores: 1,08421 ± 0,01210 es de 68%.
Como vemos, usar la distribución normal como aproximación del movimiento de la variación del precio es muy útil para realizar suposiciones.
Debemos tener en cuenta que he supuesto que la media de las variaciones del precio del EURUSD es igual o muy cercana a cero. Lo que implica que consideremos su movimiento como aleatorio (estocástico).
La distribución Lognormal y la volatilidad
Si consideramos que el movimiento de los precios se acerca a una distribución lognormal (más que a una distribución normal) podemos deducir que la variación del logaritmo neperiano de los precios sigue una distribución normal.
Por tanto, si en el apartado anterior partemos de la diferencia de los precios para calcular la desviación estándar, ahora partiremos de la diferencia de los logaritmos neperianos de los precios para calcular la desviación estándar.
Continuamos con el ejemplo anterior:
| Hora | Ask | Bid | Precio | Ln Precio | Variación horaria |
| 1:00:00 | 1,08117 | 1,08115 | 1,08116 | 0,07803 | 0 |
| 2:00:00 | 1,08215 | 1,08212 | 1,08214 | 0,07894 | 0,00090 |
| 3:00:00 | 1,08187 | 1,08184 | 1,08186 | 0,07868 | -0,00026 |
| 4:00:00 | 1,08171 | 1,08170 | 1,08171 | 0,07854 | -0,00014 |
| 5:00:00 | 1,08140 | 1,08137 | 1,08139 | 0,07824 | -0,00030 |
| 6:00:00 | 1,08124 | 1,08122 | 1,08123 | 0,07810 | -0,00014 |
| 7:00:00 | 1,08091 | 1,08091 | 1,08091 | 0,07780 | -0,00030 |
| 8:00:00 | 1,08127 | 1,08126 | 1,08127 | 0,07813 | 0,00033 |
| 9:00:00 | 1,08112 | 1,08110 | 1,08111 | 0,07799 | -0,00014 |
| 10:00:00 | 1,08162 | 1,08156 | 1,08159 | 0,07843 | 0,00044 |
| 11:00:00 | 1,08108 | 1,08105 | 1,08107 | 0,07795 | -0,00049 |
| 12:00:00 | 1,08189 | 1,08187 | 1,08188 | 0,07870 | 0,00075 |
| 13:00:00 | 1,08132 | 1,08129 | 1,08131 | 0,07817 | -0,00053 |
| 14:00:00 | 1,08129 | 1,08127 | 1,08128 | 0,07815 | -0,00002 |
| 15:00:00 | 1,08221 | 1,08199 | 1,08210 | 0,07890 | 0,00076 |
| 16:00:00 | 1,08356 | 1,08354 | 1,08355 | 0,08024 | 0,00134 |
| 17:00:00 | 1,08308 | 1,08306 | 1,08307 | 0,07980 | -0,00044 |
| 18:00:00 | 1,08379 | 1,08376 | 1,08378 | 0,08045 | 0,00065 |
| 19:00:00 | 1,08408 | 1,08406 | 1,08407 | 0,08072 | 0,00027 |
| 20:00:00 | 1,08415 | 1,08412 | 1,08414 | 0,08078 | 0,00006 |
| 21:00:00 | 1,08374 | 1,08373 | 1,08374 | 0,08041 | -0,00037 |
| 22:00:00 | 1,08408 | 1,08372 | 1,08390 | 0,08057 | 0,00015 |
| 23:00:00 | 1,08407 | 1,08395 | 1,08401 | 0,08067 | 0,00010 |
| 0:00:00 | 1,08421 | 1,08421 | 1,08421 | 0,08085 | 0,00018 |
La variación horaria es la observación muestral que utilizaremos para calcular la desviación estándar.
Un apunte, la variación horaria la hemos calculado a partir de la variación del logaritmo neperiano del precio actual y el logaritmo neperiano del precio anterior. Conociendo el cálculo de logaritmos podemos deducir que podríamos haber calculado la variación haciendo el logaritmo neperiano del precio actual dividido por el precio anterior. Y, lo más importante, el resultado se parecería mucho si lo hubiésemos calculado de la siguiente manera: Diferencia del precio actual y el anterior dividido entre la media del precio actual y el precio anterior.
En definitiva, la variación que hemos calculado no deja de ser una variación en tanto por uno de los precios (multiplicante por ciento tendríamos una variación porcentual del precio).
Ahora calculamos su desviación estándar usando la fórmula que ya conocemos: 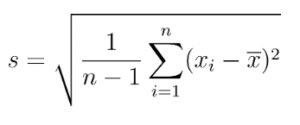
| n | 24 |
| x̄ | 0,000117378 |
| ∑(xᵢ – x̄)² | 0,000005445 |
| s horaria | 0,000486555 |
| s mensual | 0,01118019203 |
La desviación estándar de esta distribución expresada en tanto por ciento la conocemos como volatilidad.
La desviación horaria es de 0,000486555 y la mensual (multiplicante por la raíz de 528) es de 0,01118. Por tanto, y multiplicando por 100, podemos decir que la volatilidad horaria es de 0.05% y la mensual, de 1,12%.
En definitiva, existe un 68% de posibilidades de que el precio de la EURUSD se haya movido dentro del margen de ±1,12% a finales de este mes.
Hay un 95% de posibilidades de que el precio de EURUSD se haya movido dentro del margen de ±2,24% a finales de este mes.
Hay un 99,7% de posibilidades de que el precio de la EURUSD se haya movido dentro del margen de ±3,36% a finales de este mes.
Cuando nos hablan de que EURUSD tiene una volatilidad anual de 4% podemos hacer el ejercicio inverso al que hemos hecho hasta ahora y averiguar qué volatilidad mensual sería:
Volatilidad anual = 4%
Volatilidad mensual = Volatilidad anual / SQR(12) = 1,15%